Expressions and equations are fundamental concepts in mathematics that often get confused due to their similar appearance. However, the key difference between them lies in the presence of an equals sign; an equation features an equals sign between two expressions, indicating a statement of equality, while an expression does not.
What is an Expression?
- An expression is a combination of numbers, variables (letters that represent unknown numbers), and arithmetic operations (such as addition, subtraction, multiplication, and division) without an equals sign. It represents a single mathematical quantity.
- Expressions can vary from simple, involving only numbers and basic operations, to complex, including variables and multiple operations. They are fundamental in algebra and help in representing real-world scenarios mathematically.
- Key Points:
- Does not contain an equals sign.
- Can be simplified or evaluated.
- Represents a single quantity.
- Includes numbers, variables, and arithmetic operations.
What is an Equation?
- An equation is a statement of equality between two expressions, separated by an equals sign (=). It asserts that two expressions represent the same quantity under certain conditions.
- Equations can be simple or complex, linear or nonlinear, and they play a crucial role in solving problems across various fields of mathematics. Solving an equation involves finding the value(s) of the variable(s) that make the equation true.
- Key Points:
- Contains an equals sign.
- Represents a statement of equality.
- Involves finding the value of variables.
- Can be simple, linear, quadratic, or more complex.
Examples of Expressions:
Expressions can vary widely in complexity and form, such as:
- Examples:
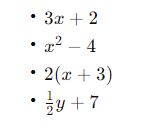
Examples of Equations:
Equations assert that two expressions are equal and typically require solving for a variable.
- Examples:

History of Expressions:
- The concept of expressions dates back to ancient civilizations, which used rudimentary forms to count and calculate.
- Historical Context:
- Originated in ancient mathematics.
- Evolved with algebraic notation.
- Became more complex with the development of algebra.
- Integral to the formulation of mathematical problems.
History of Equations:
- Equations have a rich history, starting from the simple equations in ancient Egyptian and Babylonian mathematics to the complex equations used in modern mathematics.
- Historical Context:
- Early use in solving linear and quadratic problems.
- Development of symbolic algebra in the Renaissance.
- Expansion to include complex and differential equations.
- Key to advancements in physics, engineering, and other sciences.
Similarities Between Expressions and Equations:
Both expressions and equations are fundamental to mathematics and have:
- Mathematical notation involving numbers and variables.
- The use of arithmetic operations.
- A role in representing and solving mathematical and real-world problems.
- Key Similarities:
- Utilize numbers, variables, and operations.
- Form the basis of algebra and other areas of mathematics.
- Can be manipulated according to mathematical properties.
Differences Between Expressions and Equations:
While they share some similarities, expressions and equations have distinct differences:
- Expressions are single mathematical phrases that can be evaluated or simplified but do not assert equality. Equations, on the other hand, are statements that assert two expressions are equal.
- Key Differences:
- Presence of an equals sign in equations.
- Expressions represent quantities; equations make assertions about quantities.
- Expressions are simplified; equations are solved.
- Equations can be true or false; expressions do not have truth values.
Summary – Expression vs. Equation:
Expressions and equations are staples of mathematics, each serving a unique purpose. An expression is a mathematical phrase that can represent a quantity but does not make any assertion of equality. An equation, conversely, is a statement that two expressions are equal, involving the task of finding values that satisfy this condition. Understanding the difference between these concepts is crucial for exploring more complex mathematical ideas.
Facts about Expressions
- Can include any combination of numbers, variables, and operations.
- Do not contain an equals sign.
- Serve as the building blocks for equations.
Facts about Equations
- Always include an equals sign.
- Are statements of equality between two expressions.
- Essential for solving mathematical problems.
Difference Between Expression and Equation FAQ:
- Can an expression become an equation?
- Yes, by adding an equals sign and another expression to create a statement of equality.
- What’s the main purpose of using expressions and equations?
- Expressions are used to represent quantities algebraically, while equations are used to solve for unknown values.
- Are variables required in expressions and equations?
- Yes, variables are common in both, representing unknown quantities.
- Can equations only have one solution?
- No, equations can have one, multiple, or no solutions depending on their nature.
- How do you solve an equation?
- By isolating the variable on one side to find its value.
- What role do expressions play in programming?
- In programming, expressions are used to perform calculations or represent data.
- Can an expression be converted into an equation?
- Yes, by equating it to another expression or a value.
- Are all equations linear?
- No, equations can be linear, quadratic, polynomial, etc., depending on the highest power of the variable.
- What makes an equation true?
- An equation is true when both sides have equal values.
- How do equations apply in real life?
- Equations are used in various fields like engineering, physics, and finance to solve problems involving unknown quantities.
Detailed Questions:
- What distinguishes an algebraic expression from a polynomial?
- An algebraic expression can be any mathematical phrase involving numbers, variables, and operations. A polynomial is a type of algebraic expression with variables that have non-negative integer exponents and the operations include addition, subtraction, and multiplication.
- Key Points:
- Algebraic expressions are broader, including polynomials.
- Polynomials have specific forms and restrictions on exponents.
- Both are foundational concepts in algebra.
- How does understanding expressions and equations benefit students in learning mathematics?
- Understanding these concepts helps students develop algebraic thinking, crucial for solving problems in algebra, geometry, and calculus. It lays the foundation for mathematical modeling and reasoning.
- Key Points:
- Develops algebraic thinking.
- Essential for advanced mathematical concepts.
- Aids in problem-solving and mathematical reasoning.
- In what ways do expressions and equations intersect with the study of functions?
- Expressions often define the rule of a function, and equations can determine the input-output relationship of functions. Understanding both is vital for analyzing and graphing functions.
- Key Points:
- Expressions define functions.
- Equations help in analyzing functions.
- Both are crucial for graphing and understanding functions.
- How do equations and expressions integrate into computational mathematics?
- In computational mathematics, expressions and equations are used for algorithm development, simulations, and modeling complex systems. They are fundamental in creating algorithms that solve mathematical problems computationally.
- Key Points:
- Basis for algorithm development.
- Used in simulations and modeling.
- Integral to computational problem solving.
- What are the implications of expressions and equations in the development of mathematical theories?
- They are fundamental in forming and proving mathematical theories. Expressions and equations provide a language and framework for describing patterns, relationships, and properties within these theories.
- Key Points:
- Provide a language for mathematical theories.
- Essential for describing patterns and relationships.
- Key to proving mathematical propositions.
